TheMRBconstantbeLike...
🏔️ Allegory: The Hiker and the Bouncing Trail
🏔️ Allegory: The Hiker and the Bouncing Trail
Imagine a hiker named Mira setting off on a mountain trail that zigzags wildly up and down—steep climbs followed by steep drops. The path is erratic, and with each step, she’s unsure whether she’ll go up or down next.
However, there’s something curious about this trail:
◼
With each step, the uphill and downhill sections become less extreme.
◼
Mira’s elevation bounces up and down around a certain height.
◼
Though she never walks on perfectly flat terrain, the amount she rises or falls with each step shrinks steadily.
Now, even though she never walks in a straight line, if you observed her from a distance, you’d see her trail gradually converge to a consistent elevation—a sort of average height she oscillates around more and more tightly.
That average height?
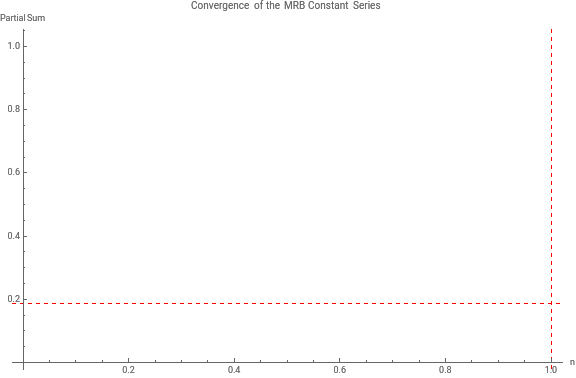
📍 That’s the MRB constant—the magical elevation Mira’s chaotic path gets closer and closer to, without ever settling exactly on it.
⛰️ The Math Behind the Trail
⛰️ The Math Behind the Trail
In the mathematical world, this trail represents the alternating sum: Each term in this sum is like a step: positive, then negative, up, then down.
The terms get smaller, just like Mira’s steps get less steep.
The total sum never settles, but it converges to a particular value—approximately 0.187859.
That value is the MRB constant—just like the hiker’s final, stable elevation.
🎯 Moral of the Allegory:
🎯 Moral of the Allegory:
The MRB constant shows how something that seems to bounce endlessly—like Mira's wild trail—can still have a stable destination, a converging behavior, as long as the steps (terms) get small enough.
terms=20;(*Generatethepartialsums*)partialSums=Accumulate[Table[(-1)^k(k^(1/k)-1),{k,1,terms}]];(*Createaninteractiveplotwithpointsturningredoneatatime*)Animate[ListLinePlot[{partialSums,Style[partialSums[[1;;n]],Red]},PlotMarkersAutomatic,PlotStyleBlue,GridLines{{1},{0.187859}},GridLinesStyleDirective[Red,Dashed],PlotRangeAll,AxesLabel{,},PlotLabel,ImageSizeLarge],{n,1,Length[partialSums],1},AnimationRate0.5]
Out[]=
Manipulate